How S-DES Works
Abstract
Data Encryption Standard (DES) is
one of the most widely used symmetric key cryptography algorithm. Therefore,
the susceptibility of DES to different kind of attacks has been a concern since
the algorithm was first made public. The problem has escalated to the point
that Electronic Frontier Foundation has now built a DES cracking machine, at a
cost of less than 250,000 USD, that can find the right key in about three days.
Of course, the cryptanalytic technique used to find this key might seem overwhelming
for us as students to learn. Hence, we need a simpler version of DES in order
to learn about these cryptanalytic techniques, S-DES is the answer. S-DES is
simpler version of DES that operates on 8-bit message blocks and 10-bits key.
This paper discuss about S-DES design, how S-DES works, and different kind of
attacks on S-DES.
Introduction
S-DES is a simpler version of the
DES algorithm. S-DES operates on 8-bit message blocks and 10- bits key. It was
designed as a test block cipher for learning about modern cryptanalytic
techniques such as linear cryptanalysis, differential cryptanalysis, and
linear-differential cryptanalysis. The same key is used for encryption and
decryption. With its 10-bits key, comparing to 56-bits key used by DES, S-DES
is much more vulnerable to an attack. Different kind of attacks that have been
proven successful to reveal S-DES key or subset of key are brute force attack,
chosen plain text attack, chosen cipher text attack, and known plain text
attack.
S-DES
S-DES operates on 8-bit message
blocks and 10-bits key. It consists of three steps: initial permutation, two
rounds key-dependent computation, and inverse of initial permutation. The
10-bit key is used to generate two different blocks of 8-bit sub keys. The
first block is used in the first round of key-dependent permutation and the
second block is used in the second round. First, the 10-bit key is subject to
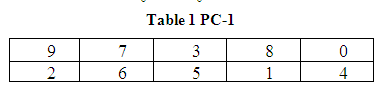
an initial permutation, Permuted Choice 1 which is determined by table PC-1, to
generate two 5-bit blocks named A0 and B0.
There are two rows in the table. The
first row determines the bits of A0 and the second row determines
the bits of B0. Thus, the bits of A0 are bits 9, 7, 3, 8,
0 of 10 -bit key and the bits of B0 are bits 2, 6, 5, 1, 4 of 10-bit
key. Second, a single left shift is performed on A0 and B0
yielding A1 and B1. Third, B1 is concatenated
to A1 and then subjected to the second permutation, Permuted Choice
2 which is determined by table PC-2, to form the first block of 8-bit sub keys
named K1.
Thus, the bits of K1 are
bits 3, 1, 7, 5, 0, 6, 4, and 2 of bits of A1B1. Fourth,
a two left shifts is performed on A1 and B1 yielding A2
and B2. Fifth, B2 is concatenated to A2 and
then subjected to the second permutation, Permuted Choice 2,
to form the second block of 8-bit sub keys named K2.
Figure
1 S-DES Key Generation
The encryption procedure can be
summarized as:
Where,
C :
cipher text
P :
plain text
K :
10-bit key
IP :
initial permutation
IP-1 : inverse of initial permutation
ρ1 : first round of key dependent
Computation
ρ2 : second round of key dependent
Computation
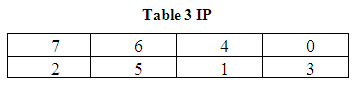
First, the 8-bit message block is
subjected to an initial permutation, IP, which is determined by table IP, to
generate two 4-bit blocks named L0 and R0.
There are two rows in the table. The
first row determines the bits of L0 and the second row determines
the bits of R0. Thus, the bits of L 0 are bits 7, 6, 4, 0
of 8-bit message block and the bits of R0 are bits 2, 5, 1, 3 of
8-bit message block. Second, L0 and R0 are subjected to
first round of key dependent computation yielding L1 and R1,
which can be summarized as follows:
where,
f : key dependent cipher function
(will be explained bellow)
Third, L1 and R1
are subjected to second round of key dependent computation yielding L2
and R2, which can be summarized as follows:
Fourth, R2 is
concatenated to L2 and then subjected to the second permutation, IP-1
which is inverse of initial permutation. The result of this last step is
ciphered 8-bit message block corresponding to the input.
Figure
2 S-DES Encryption Procedure
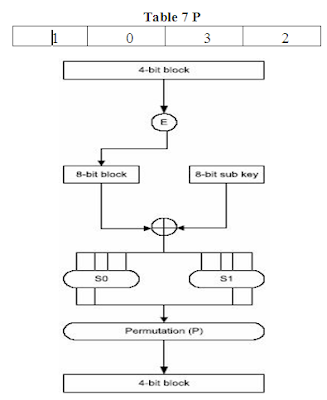
The first step of key dependent cipher function, f, is to pass the 4-bit block input to function E. E is a function which takes 4- bit block input and yields a 8-bit block as output according to table:
The
8-bit block then XORed with the 8- bit sub key, K1 for first round
and K2 for second round. The result of this XORing operation is then
split into two 4-bit blocks, the first four bits from the most significant bit
being C0 and the remaining bits being C1. C0
and C1 are then applied to S0 and S1
respectively. S0 and S1 are S-Boxes which take in a 4-bit
input and yield a 2-bit output.
An
example of how to get output using S0 and 1001 as input is as
follows: we take the first bit and the last bit of 1001 and then used this
result to represent a number in base 2, in which we get 3 (11 equals to 3 in
base 2). 3 is the row number we are looking for. Then we take the middle two
bits of 1001 and then, same as above, used this result to represent a number in
base 2, in which we get 0 (00 equals to 0 in base 2). 0 is the column number we
are looking for. The element of 3rd row and 0th column is
1, which in binary is written as 01. Hence, using 1001 as input, we get 01 as
the output. The output of S0 and S1 are concatenated and
then subjected to a permutation, P, which is determined by table P. The result
of this last step becomes the result of key-dependent cipher function f.
Figure 3 S-DES Key Dependent Cipher
Function
The decryption procedure is the same
as the encryption procedure, but the sub keys are applied in the reverse order.
K2 is used in the first round and K1 is used in the
second round.
Attack On S-DES
It is feasible to attack S-DES using
brute force attack since it only has a key size of 10 bits. In order to perform this kind of attack,
we need to have a plain text-cipher text pair in which we search the key space
until the appropriate plain text encrypted with the guessed key yields the
cipher text.
Differential cryptanalysis is a
chosen plain text/chosen cipher text attack. Chosen plain text attack is
a scenario in which the attacker has the
ability to chose plain text and to view their corresponding cipher text. Chosen cipher text attack is a scenario in which the attacker has ability to choose cipher text and to view their corresponding
plain text. Differential cryptanalysis involves the analysis of the effect of
the plain text pair difference on the resulting cipher text difference. In
S-DES, the difference in a cipher text pair for a specific difference of a
plain text pair is influenced by the key. By utilizing this fact, we can reveal
information about the key 1).
Linear
cryptanalysis is a known plain text attack.
Known
plain text attack is
a scenario in which the attacker has
access to the pairs (Pi, Ci), i = 1, . . .N of known plain texts and their
corresponding cipher texts. Linear cryptanalysis is based on the fact that
there are high probability of occurrences of linear expressions consisting the
plain text bits, cipher text bits, and key bits. The goal is to find the linear
expression which holds with the highest linear probability bias. A linear
expression consisting the plain text bits, cipher text bits, and key bits with
a high linear probability bias means that the cipher used is not sufficiently
random. Using the linear expression with the highest linear probability bias
obtained, we can reveal information about the key 5).
Conclusion
In this paper, we have shown the
design issue of S-DES and how it works in enciphering and deciphering message.
With 10-bits key, different kind of attacks have been done successfully on
S-DES. These including brute force attack, chosen plain text attack, chosen
cipher text attack, and known plain text attack. Having this kind of
characteristic, we can use S-DES as a first step in learning about
cryptanalytic technique. Furthermore, this technique can also be used to attack
more complicated cryptography algorithm, in this case it will be DES.
References
:
- E.Biham and A.Shamir, Differential Cryptanalysis of the Data Encryption Standard, Springer-Verlag, 1993.
- Electronic Frontier Foundation, Cracking DES: Secrets of Encryption Research, Wiretap Politics, & Chip Design, O’Reilly and Associates, 1998.
- J.Killian and P.Rogaway, How to Protect DES Against Exhaustive Key Search, Advances in Cryptology-CRYPTO ’96, Lecture Notes in Computer Science, Springer-Verlag, 1996.
- K.S.Ooi and Brain Chin Vito, Cryptanalysis of S-DES, University of Sheffield Centre, Taylor’s College, 2002.
- M.Matsui, Linear Cryptanalysis Method for DES cipher, EUROCRYPT,1994.
0 komentar: